Collision detection is one of the most complex and challenging parts of game programming, and is often the key area where performance is usually lost. To solve this, we have a lot of structures that eliminate unnecessary checks for collisions, like QuadTrees, Grids, BSP Trees, OcTrees, etcetera. In this post, we are going to study about AABB Trees, which are extremely fast for finding collisions.
Special thanks to the original Box2D author Erin Catto, and Bullet3D author Nathanael Presson for their open source implementations of AABB Tree. I used the original sources of Box2D as inspiration in studying this data structure.
AABB Trees, what are they?
An AABB tree is nothing but simply a binary tree, where all the AABBs are stored at the leaves. The main advantage for this kind of broad-phase is that this is a border-less data structure, and it doesn’t require you to explicitly specify an area which other kinds of data structures such as grids or QuadTrees require. They are better understood by looking at a visual rather than reading text, so here it is.
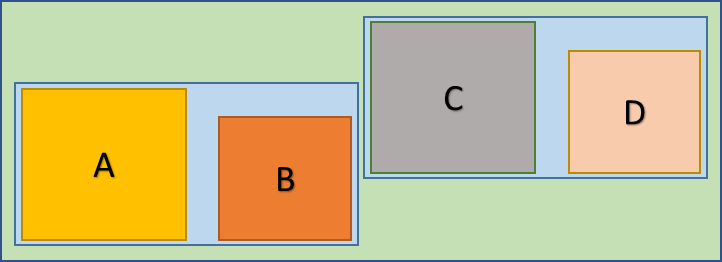
Assume that you have the above scene of objects, and A, B, C and D are the AABBs that wrap the objects in the scene. As said already, we have the AABBs that represent the objects only at the leaves. But still, all the intermediary nodes also have the AABBs, and they are just combined AABBs of their children. To allow for delayed re-insertions of the AABBs when they move, their parents use a bit of padding around them. The same above scene looks like this in hierarchy view.
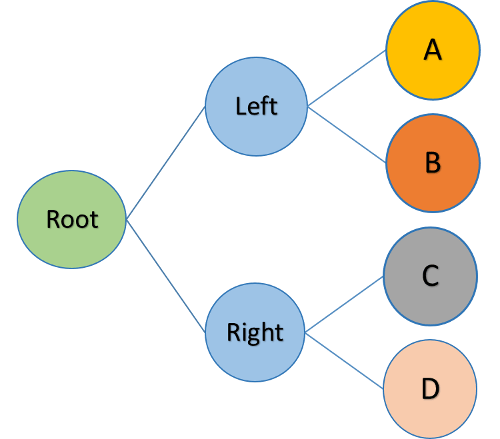
The root AABB will contain all the child AABBs, the left node’s AABB will contain AABBs A and B, and the right node’s AABB will contain AABBs C and D. So querying from this data structure will be extremely fast. However let us go through the node data structure first.
The Node in the AABB Tree
I am not going to give you the complete code of the implementation, but only give psuedocode and describe how the data works. Though the original implementations keep the nodes in an array based representation, we are going to implement it in a linked-list based representation. The structure of the node will be as follows.
struct Node
{
// The link to the parent Node
struct Node* parent;
// The AABB of the current Node
struct AABB aabb;
// The left and right children
struct Node* left;
struct Node* right;
// The user data, can be used to identify the nodes
void* userData;
// The height, for maintaining balance
int height;
};
Each node will have a parent (NULL for the root node), an AABB covering it, children (NULL for leaf nodes) and user data (NULL for intermediary nodes). I will first cover querying from the tree and then start about insertion and deletion of the nodes.
Querying from the AABB Tree
The querying is the simplest operation on the AABB tree, the user passes the root node, an AABB and a list, and the query function will add all the leaf nodes that intersect with the provided AABB into the list.
void aabbTreeQuery(struct Node* node, struct AABB aabb, struct List* list)
{
// Test for NULL node
if (node == NULL)
return;
// Only process the node if it intersects the given AABB
if (aabbIntersect(node->aabb, aabb))
{
if (node->left == NULL && node->right == NULL)
{
// It is a leaf node, add it to the list
listAdd(list, node);
}
else
{
// Query the child nodes recursively
aabbTreeQuery(node->left, aabb, list);
aabbTreeQuery(node->right, aabb, list);
}
}
}
This is how simple it can be. We start with the root node, test if the root node’s AABB intersects with the AABB provided. If it intersects then only the node is processed. When there are a lot of entities and we did properly balance the tree, we can keep these tests to be the minimum.
Inserting of AABBs
This is the most important part of the AABB tree, and here, we are going to not only insert the AABB, but also update the respective parents and combine the AABB of the parents so that our querying will work. The insert function will return the newly created node pointer which the user can cache.
struct Node* aabbTreeInsert(struct Node** root, struct Node* node)
{
node->left = NULL;
node->right = NULL;
node->parent = *root;
node->height = 0;
// If the root is NULL, create the node and set it to the root
if (*root == NULL)
*root = node;
// If the root is a leaf node, replace root with a temporary parent
else if (*root->left == NULL && *root->right == NULL)
{
struct Node* newParent = (struct Node*) malloc(sizeof(struct Node));
newParent->parent = *root->parent;
newParent->left = *root;
newParent->right = node;
// Replace links in newParent's parent
if (newParent->parent->left == *root)
newParent->parent->left = newParent;
else
newParent->parent->right = newParent;
}
// Otherwise we have to select whether to insert in left or right
else
{
// TODO!! We have to find where to insert, left or right?
}
aabbTreeRecalculateUp(node);
// Return the node
return node;
}
Woah, now we have an issue, where should we insert it? To the left? Or to the right? This looks tricky for us, but no it is not. To get after this issue, we employ a cost function, and find the costs of inserting it into the left and right children. Then we insert it into the child which gives the minimum cost.
Okay, this is cool, you might say, but what is the cost function? How can we choose it? For integers we can choose some sort of hash function, but for AABBs? We are going to use the perimeter of the AABB as the cost function. We first set a temporary AABB to be a combined AABB of the node with the left child and also the right child. Every time we calculate the perimeter of the combined AABB and select the minimum cost.
// We need to propagate down until we find the leaf node
struct Node* parent = *root;
// Loop until parent becomes a leaf node
while (parent->left != NULL || parent->right != NULL)
{
struct AABB combinedAABB;
float cost1, cost2;
// Test the cost with left child
combinedAABB = aabbCombine(node->aabb, parent->left->aabb);
cost1 = aabbPerimeter(combinedAABB);
// Test the cost with the right child
combinedAABB = aabbCombine(node->aabb, parent->right->aabb);
cost2 = aabbPerimeter(combinedAABB);
if (cost1 < cost2)
parent = parent->left;
else
parent = parent->right;
}
// Insert in parent
return aabbTreeInsert(&parent, node);
So that is how we insert a new node into the AABB tree. It might look so heavy, but in fact it is actually very easy. At the end we call the aabbTreeRecalculateUp function, which starts at the node, and walks up in the hierarchy fixing the AABBs and the tree heights. It will also make a call to aabbTreeBalance after doing it, so our tree remains balanced.
Removing a node from the tree
The removing process is actually quite simple, since the nodes are always leaf nodes, we can quite easily remove the nodes. All we have to do is to free the node, and set it’s reference to NULL. Let us see it in code now.
void aabbTreeRemove(struct Node** root, struct Node* node)
{
struct Node* parent = node->parent;
// If the node is root, then parent will be NULL
if (parent == NULL)
{
free(node);
*root = NULL;
return;
}
// Replace the parent with sibling
struct Node* sibling = NULL;
if (parent->left == node)
sibling = parent->right;
else
sibling = parent->left;
// Check if there is a grandparent
if (parent->parent != NULL)
{
struct Node* grandParent = parent->parent;
if (grandParent->left == parent)
grandParent->left = sibling;
else
grandParent->right = sibling;
sibling->parent = grandParent;
free(parent);
free(node);
}
// Parent is the root, replace root with sibling
else
{
*root = sibling;
sibling->parent = NULL;
}
aabbTreeRecalculateUp(sibling);
}
And that is all there is to it. We now know how to delete a node in the tree. We are almost done, except for the one thing, balancing the tree. The tree balance needs to be done just like how you would balance an AVL tree, by checking the height. Once this is done, congratulations, you now have a powerful broad-phase data structure.
A small word of warning is that all the code here is written from my mind, and is not tested. My implementation for my game engine is done in Java, and is implemented in the form of array representation just like the original Box2D code.
