వీడియో గేమ్ ప్రోగ్రామింగ్ లో collision detection అనేది చాలా సంక్లిష్టమైన అంశం. అంతే కాకుండా ఇక్కడే చాలా performance సంపాదించుకోవచ్చు. ఇందుకోసం మనకి అనవసరమైన కంపారిజన్స్ ని వదిలేసే చాలా డాటా స్ట్రక్చర్లు ఉన్నాయి, QuadTrees, Grids, BSP Trees, OcTrees వంటివి వీటికి మంచి ఉదాహరణలు. ఈ పోస్టులో మనం collisions ని చాలా వేగంగా కనిపెట్టే AABB Trees గురించి చదువుదాం.
Erin Catto (Box2D) కి మరియు Nathanael Presson (Bullet3D) కి వారి ఒరిజినల్ ప్రాజెక్టులను open-source గా విడుదల చేసినందుకు కృతజ్ఞతలు తెలుపుకుంటున్నాం. ఈ డాటా స్ట్రక్చర్ ని చదివేందుకు వాటిని స్ఫూర్తి గా తీసుకోవడం జరిగింది.
AABB Trees అంటే ఏమిటి?
ఈ AABB Tree అనేది మనం మామూలుగా ఉపయోగించే binary tree లాంటిదే, కాకపోతే ఇక్కడ మనం మన AABB లను leaf nodes లో ఉంచుతాం. దీని వల్ల మనకి కొన్ని ఉపయోగాలున్నాయి. అదేంటి అంటే మనం మిగిలిన collision డాటా స్ట్రక్చర్లతో పోలిస్తే ఇందులో పరిధులను ఉంచనవసరం లేదు. దీనిని చెప్పేకంటే చూపిస్తే బాగా అర్థమవుతుంది, ఈ బొమ్మ ను చూడండి.
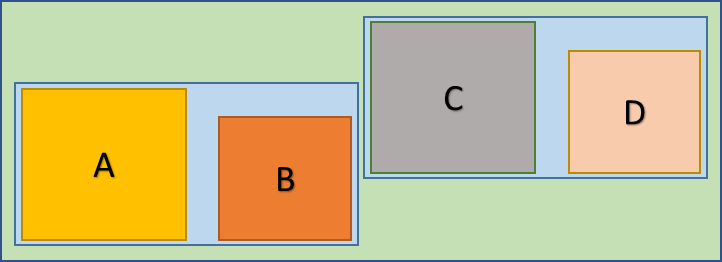
మీ వద్ద పైన చూపిన విధంగా ఒక scene ఉంది అనుకోండి. అందులో A, B, C మరియు D లు మన గేంలోని క్యారెక్టర్లను కలిగి ఉండే AABB లు అనుకోండి. ముందే చెప్పిన విధంగా మన ట్రీలో AABB లు చివరలో ఉంటాయి, అంటే leaf nodes అన్నమాట. అయినప్పటికీ మనం మధ్యలోని నాడులకి కూడా AABB లను తమ కింది వాటిని కలిగి ఉండేలా అమర్చుతాం. అంతే కాకుండా ప్రతీసారీ కదిలిన వాటిని తీసివేయాల్సిన అవసరం లేకుండా మధ్యలోని నాడులని కొంత వదులుగా చేస్తాం. అదే మీరు ఈ క్రింది బొమ్మలో చూడచ్చు.
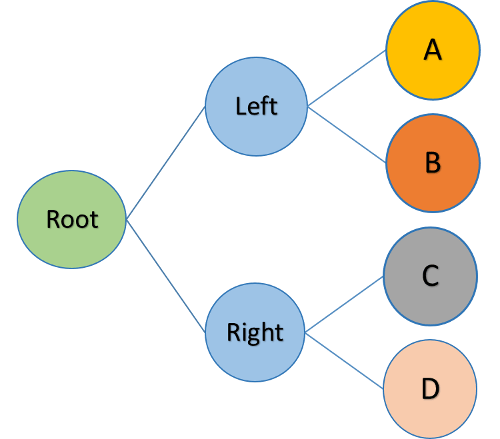
ఇక్కడ మీరు చూసినట్లైతే A మరియు B అనేవి ఎడమ నాడివి, అలాగే C మరియు D అనేవి కుడి నాడికి చెందినవి. ఇందువలన మనకు వీటి లోనుండి కంపారిజన్స్ చాలా వేగంగా జరుగుతాయి. ఇప్పుడు మనం మన node ని ఎలా రిప్రెజెంట్ చేస్తామో చూద్దాం.
నోడ్ ని కోడ్ లో ఎలా వ్రాయాలి?
నా మిగతా టూటోరియల్స్ లాగానే ఇక్కడ కూడా నేను మీకు అసలైన కోడ్ ని ఇవ్వను. నేను మీకు psuedocode ని మాత్రమే ఇస్తాను, మరియు మీకు ఇది ఎలా పని చేస్తుందో వివరిస్తాను. దీన్ని మూలంలో array లను ఉపయోగించి వ్రాసినా, మనం ఇప్పుడు దీన్ని linked-list విధానం లో వ్రాద్దాం. ఆ కోడ్ ఇలా ఉంటుంది.
struct Node
{
// The link to the parent Node
struct Node* parent;
// The AABB of the current Node
struct AABB aabb;
// The left and right children
struct Node* left;
struct Node* right;
// The user data, can be used to identify the nodes
void* userData;
// The height, for maintaining balance
int height;
};
ప్రతి నాడికి ఒక పేరెంట్, ఒక AABB, పిల్ల నాడులు, ఒక డాటా ఫీల్డ్ ఉంటాయి. మొదటి నాడి (root నోడ్) కి NULL పేరెంట్ అవుతుంది. అలాగే leafs కి పిల్ల నాడులు ఉండవు. ముందు నేను మీకు queries ఎలా చేయాలో చెప్పి ఆ తరువాత insert చేయడం, delete చేయడం ఎలాగో వివరిస్తాను.
AABB tree నుండి query చేయడం ఎలా?
AABB tree నుండి query చేయడం అన్నింటి కన్నా చాలా సులభమయిన పని. ఈ ఫంక్షన్ కి మనం root ని, మనం వెతకాల్సిన పరిధులని, మరియు ఒక లిస్టును ఇస్తే intersect అయ్యే అన్ని AABBలను ఆ లిస్టులోకి చేరుస్తుంది. ఎలాగో మీరే చూడండి.
void aabbTreeQuery(struct Node* node, struct AABB aabb, struct List* list)
{
// Test for NULL node
if (node == NULL)
return;
// Only process the node if it intersects the given AABB
if (aabbIntersect(node->aabb, aabb))
{
if (node->left == NULL && node->right == NULL)
{
// It is a leaf node, add it to the list
listAdd(list, node);
}
else
{
// Query the child nodes recursively
aabbTreeQuery(node->left, aabb, list);
aabbTreeQuery(node->right, aabb, list);
}
}
}
ఇంత కన్నా సులభంగా మరేదీ ఉండదు. మనం root తో మొదలు పెట్టి root యొక్క AABB మన పరిధి లోనే ఉందో లేదో చూస్తాం. ఇలా ప్రతీ నోడ్ లోనూ అది మనం వెతికే పరిధులలో ఉంటే దాన్ని మాత్రమే ప్రాసెస్ చేస్తాం. ఈ విధానంలో మన దగ్గర చాలా entities ఉన్నప్పటికీ మనం మన tree ని బాలన్స్ చేస్తాం కాబట్టి మనం చాలా తక్కువ కంపారిజన్స్ చేస్తాం.
AABB లను ఇన్సర్ట్ చేయడం ఎలా?
ఇప్పుడు మనం AABB లను ఇన్సర్ట్ చేయడం ఎలాగో చూద్దాం. ఇక్కడ మనం ఇన్సర్ట్ చేయడం మాత్రమే కాకుండా ఇన్సర్ట్ చేసిన తరువాత నాడి లోని లింక్స్ ను కూడా సరి చేస్తాం. ఈ ఇన్సర్ట్ ఫంక్షన్ మనకు ఇన్సర్ట్ చేసిన కొత్త నాడి యొక్క పాయింటర్ ను తిరిగిస్తుంది. ఇప్పుడు మనం ఆ కోడ్ ను చూద్దాం.
struct Node* aabbTreeInsert(struct Node** root, struct Node* node)
{
node->left = NULL;
node->right = NULL;
node->parent = *root;
node->height = 0;
// If the root is NULL, create the node and set it to the root
if (*root == NULL)
*root = node;
// If the root is a leaf node, replace root with a temporary parent
else if (*root->left == NULL && *root->right == NULL)
{
struct Node* newParent = (struct Node*) malloc(sizeof(struct Node));
newParent->parent = *root->parent;
newParent->left = *root;
newParent->right = node;
// Replace links in newParent's parent
if (newParent->parent->left == *root)
newParent->parent->left = newParent;
else
newParent->parent->right = newParent;
}
// Otherwise we have to select whether to insert in left or right
else
{
// TODO!! We have to find where to insert, left or right?
}
aabbTreeRecalculateUp(node);
// Return the node
return node;
}
ఇప్పుడు మనం ఒక సమస్య గురించి మాట్లాడుకుందాం. మనం మన కొత్త నాడిని ఎటు వైపున ఇన్సర్ట్ చేయాలి? ఎడమ వైపు చేయాలా? లేక కుడివైపు చేయాలా? ఇది కొంత జటిలమైనదిగా అనిపించవచ్చు, కానీ కాదు, ఇది చాలా సులభమైన సమస్య. దీని కోసం మనం ఒక cost ఫంక్షన్ని ఉపయోగిస్తాం. దాన్ని ఉపయోగించి ఎడమవైపున ఇన్సర్ట్ చేస్తే cost ఎంత, కుడివైపున ఇన్సర్ట్ చేస్తే cost ఎంత అని కనుక్కుని ఆ తరువాత ఎటువైపు తక్కువ cost ఉంటుందో అటువైపున ఇన్సర్ట్ చేస్తాం.
అంతా బాగానే ఉంది కానీ ఈ cost ఫంక్షన్ అంటే ఏంటి? దాన్ని మనం ఎలా ఎంచుకోవాలి? ఇంటీజర్స్ కి అయితే మనం ఒక హాష్ ఫంక్షన్ ని ఉపయోగించవచ్చు, కానీ ఒక AABB కి cost ని ఎలా కనుక్కోవడం? అందుకోసం మనం ఇక్కడ ఆ AABB యొక్క చుట్టుకొలతను ఉపయోగించబోతున్నాం. మనం ముందు ఒక టెంపరరీ AABB ని ఉపయోగించి ఎడమవైపున అయితే cost ఎంత, కుడివైపున అయితే cost ఎంత అని చూసి ఎటువైపున తక్కువగా ఉంటే అటువైపున ఇన్సర్ట్ చేస్తాం.
// We need to propagate down until we find the leaf node
struct Node* parent = *root;
// Loop until parent becomes a leaf node
while (parent->left != NULL || parent->right != NULL)
{
struct AABB combinedAABB;
float cost1, cost2;
// Test the cost with left child
combinedAABB = aabbCombine(node->aabb, parent->left->aabb);
cost1 = aabbPerimeter(combinedAABB);
// Test the cost with the right child
combinedAABB = aabbCombine(node->aabb, parent->right->aabb);
cost2 = aabbPerimeter(combinedAABB);
if (cost1 < cost2)
parent = parent->left;
else
parent = parent->right;
}
// Insert in parent
return aabbTreeInsert(&parent, node);
ఈ విధంగా మనం కొత్త నాడులని ఇన్సర్ట్ చేస్తాం. ఇది మీకు కొంచెం క్లిష్టంగా అనిపించవచ్చుకానీ నిజానికి ఇది చాలా సులభమైనది. ఈ ఫంక్షన్ చివరలో మనం aabbTreeRecalculateUp అనే ఫంక్షన్ ని ఉపయోగిస్తాం, అది మన AABB Tree లోని ప్రతి నాడి వద్ద లింకులను మరియు height లను సరిచేస్తుంది. అంతే కాకుండా మనం తరువాత aabbTreeBalance అనే ఫంక్షన్ ని ఉపయోగించి మన ట్రీను బాలన్సుడుగా ఉంచుతాం.
ట్రీనుండి నాడిని తొలగించడం
నాడులను తొలగించే విధానం చాలా సులభమైనది. మన నాడులన్నీ ఎప్పుడూ లీఫ్ నోడ్స్ అయినందువల్ల మనం వాటిని చాలా సులభంగా తొలగించవచ్చు. మనం చేయాల్సినదంతా కేవలం నాడిని free చేసి దాని రిఫరెన్స్ ను NULL గా చేయడమే. ఆ కోడ్ ను మనం ఇప్పుడు చూద్దాం.
void aabbTreeRemove(struct Node** root, struct Node* node)
{
struct Node* parent = node->parent;
// If the node is root, then parent will be NULL
if (parent == NULL)
{
free(node);
*root = NULL;
return;
}
// Replace the parent with sibling
struct Node* sibling = NULL;
if (parent->left == node)
sibling = parent->right;
else
sibling = parent->left;
// Check if there is a grandparent
if (parent->parent != NULL)
{
struct Node* grandParent = parent->parent;
if (grandParent->left == parent)
grandParent->left = sibling;
else
grandParent->right = sibling;
sibling->parent = grandParent;
free(parent);
free(node);
}
// Parent is the root, replace root with sibling
else
{
*root = sibling;
sibling->parent = NULL;
}
aabbTreeRecalculateUp(sibling);
}
అంతకుమించి ఇక్కడ మరింకెమీ లేదు. ఇప్పుడు మనం నాడులను తొలగించడం ఎలాగో కూడా తెలుసుకున్నాం. ఇంక ఒకే ఒక్క విషయం మిగిలుంది, ట్రీని బాలన్స్ చేయడం. దాన్ని మనం AVL ట్రీలో ఎలా ఎత్తుని ఉపయోగించి చేస్తామో ఇక్కడ కూడా అదే విధంగా చేస్తాం. మన నాడులలో ఎత్తును ఒక ఫీల్డ్ గా పెట్టిన కారణమే అది. ఈ టూటోరియల్ను విజయవంతంగా ముగించినందుకు శుభాకాంక్షలతో ఇంతటితో ముగిస్తున్నాను. మీ దగ్గర ఇప్పుడు ఒక పవర్ఫుల్ డాటా స్ట్రక్చర్ ఉంది.
చివరిగా ఒక చిన్న మాట: ఇక్కడ ఉన్న కోడ్ అంతా నేను స్వంతంగా గుర్తుపెట్టుకుని వ్రాసింది. దీన్ని ఏమాత్రం టెస్ట్ చేయలేదు. నేను నా ఇంజిన్లో దీన్ని Java లో, అసలైన Box2D కోడ్ లో వ్రాసిన విధంగా array విధానంలో వ్రాసాను.
